知识杂记-1

Posted on Edited on In Views: Disqus:

近期读了一些MP（Motion Planning）方向的论文，其用到了一些图形学，数学方面的知识，遂小记，以便于日后复习。

NTFields: Neural Time Fields for Physics-Informed Robot Motion Planning

Progressive Learning for Physics-informed Neural Motion Planning

PC-Planner: Physics-Constrained Self-Supervised Learning for Robust Neural Motion Planning with Shape-Aware Distance Function

线性插值

  • 线性插值
  • 二线性插值
  • 三线性插值

转载自线性插值与双/三线性插值 - 知乎 (zhihu.com)

线性插值 linear interpolation

无需多言，公式：

img

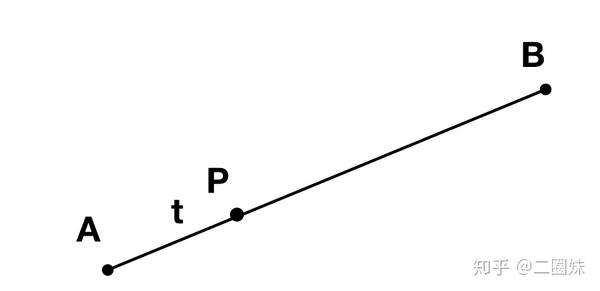
P(t) = A + (B -A)t

P(t) = A(1-t) + Bt

这个函数一般我们叫做lerp.

1
2
3
template<typename T>
inline T lerp(const T &lo, const T &hi, float t)
{ return lo * (1 - t) + hi * t; }

如果门把t变成某个函数g(t)，那么线性可以变得平滑，可以变成多项式等等…

双线性插值 bilinear interpolation

img

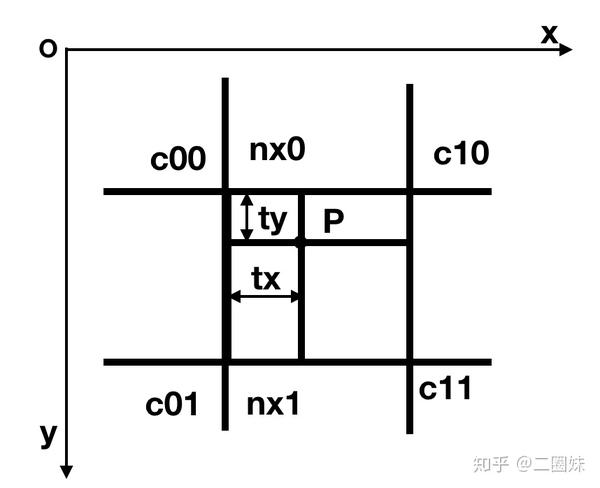
思路是类似的，我们首先用插值算出 nx0 和 nx1，然后再用插值算出P处的值：

nx0 = lerp(c00,c10,tx)

nx1 = lerp(c01,c11,tx)

p = lerp(nx0,nx1,ty)

如果我们展开的话长这样：

p=c00(1−tx)(1−ty)+c10tx(1−ty)+c01(1−tx)ty+c11txty

三线性插值 Trilinear interpolation

同样的思路，只是我们推到3d空间：

img

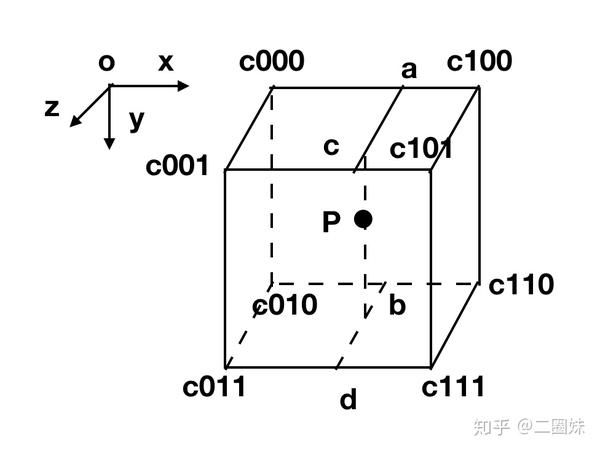
a = lerp(c000,c100,tx)

b = lerp(c010,c110,tx)

c = lerp(c001,c101,tx)

d = lerp(c011,c111,tx)

得到了这四个点，再把它代入回双线性插值既可：

img

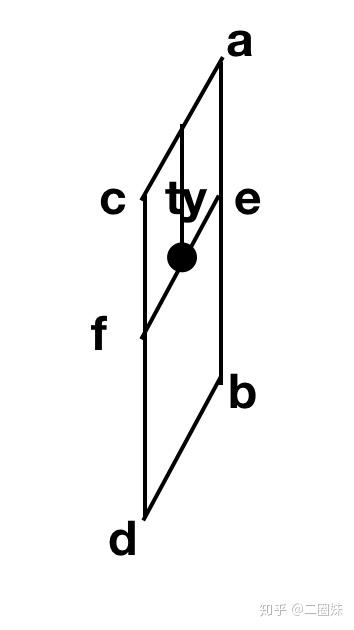
e = lerp(a, b, ty)

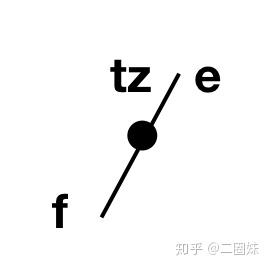
f = lerp(c, d, ty)

最终e, f之间构成了线性插值：

img

拉普拉斯算子

在知乎看到了一个很好的回答，引用在此为什么 空间二阶导（拉普拉斯算子）这么重要？ - 链巨人的回答

“我们进一步概括，在一连串的事件中，拉普拉斯算子能够计算找到那些变化很突然的那些事件。这便是拉普拉斯得到很多应用，很重要的原因。”

Grid_sample

torch.nn中的方法

1
torch.nn.functional.grid_sample(input, grid, mode='bilinear', padding_mode='zeros', align_corners=None)

简单来说，grid_sample提供一个input以及一个网格，然后根据grid中每个位置提供的坐标信息(input中pixel的坐标)，将input中对应位置的像素值填充到grid指定的位置，得到最终的输出。

具体介绍引用一个知乎回答TORCH.NN.FUNCTIONAL.GRID_SAMPLE - 知乎 (zhihu.com)

SDF(Signed Distance Field)

SDF(signed distance field)基础理论和计算 - 知乎 (zhihu.com)

浅谈3D隐式表示（SDF，Occupancy field，NeRF）-CSDN博客

SE(2) SE(3)

SE(2) 和 SE(3) 是描述刚体运动的李群（Lie group），常用于机器人学、计算机视觉和图形学等领域。

  1. **SE(2)**：

    • 表示二维空间中的刚体运动，包括平移和旋转。
    • 具体来说，SE(2) 是由所有的平移（x, y）和旋转（θ）组成的组合。
    • 数学上，可以表示为：
      $SE(2) = { (x, y, \theta) | x, y \in \mathbb{R}, \theta \in [0, 2\pi) }$

  2. **SE(3)**：

    • 表示三维空间中的刚体运动，包括平移和旋转。
    • SE(3) 包含一个三维平移向量（x, y, z）和一个旋转矩阵（通常表示为四元数或欧拉角）。
    • 数学上，可以表示为：
      $SE(3) = { (x, y, z, R) | (x, y, z) \in \mathbb{R}^3, R \in SO(3) }$
    • 其中，SO(3) 是表示三维空间中所有旋转的特殊正交群。

这两个空间提供了描述物体在平面和空间中运动的数学框架，广泛应用于运动学分析和路径规划等问题。